A闪的 BLOG 技术与人文

扇形内求正方形边长

最近给公司社区做了一个抽奖用的插件，前端效果制作时遇到一个小小的几何体。很有意思，这里记录。

需求：在一个已知半径r且夹角小于180度的扇形内，计算出最大面积正方形。这里有一个小小的规则，以扇形角平分线做射线，其射线于正方形两条边垂直。

做图效果如下：

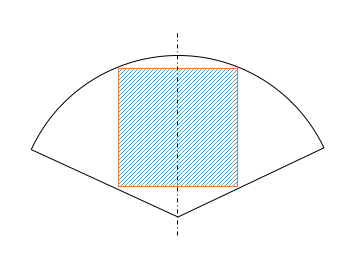
计算方法非常简单，需要做一点点简单的“改变”，就能够方便的求出正方形边长。

先对我们的扇形做辅助线

根据勾股定理，我们可以得到如下两个公式：

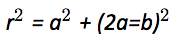
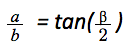
解这个二元一次方程组就比较省事了，我们做代入换算，将b消掉，只保留a。最终得到a的计算公式。

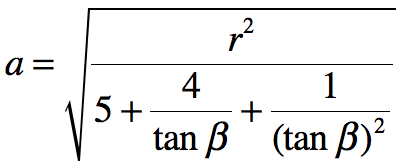
得到了a，就得到了一切。我们使用编码将其计算出来，计算代码如下：

class Main extends egret.DisplayObjectContainer {

    public constructor() {
        super();
        this.init();
    }

    private angle = 10;
    private speed = 1;
    private step = 1;
    private cp:egret.Point = new egret.Point(200,250);
    private shp:egret.Shape;
    private r:number = 200;

    private init()
    {
        var bg:egret.Shape = new egret.Shape();
        bg.graphics.beginFill(0xffffff);
        bg.graphics.drawRect(0,0,400,300);
        bg.graphics.endFill();
        this.addChild(bg);

        this.shp = new egret.Shape();
        this.shp.x = this.cp.x;
        this.shp.y = this.cp.y;
        this.addChild(this.shp);

        this.addEventListener(egret.Event.ENTER_FRAME,this.change,this);
    }
    private change(evt:egret.Event)
    {
        if(this.angle<=10)
        {
            this.speed =  this.step;
        }
        else if(this.angle>=160)
        {
            this.speed =  this.step*-1;
        }
        this.angle += this.speed;
        this.draw();
    }

    private draw()
    {
        this.shp.graphics.clear();
        var startAng = Math.PI/180*(180+(180-this.angle)/2);
        var endAng = Math.PI/180*(180+(180-this.angle)/2+this.angle);

        this.shp.graphics.beginFill(0xcccccc);
        this.shp.graphics.drawArc(0,0,this.r,startAng,endAng);
        this.shp.graphics.lineTo(0,0);
        this.shp.graphics.endFill();
        this.shp.graphics.lineStyle(1,0);
        var beta = Math.PI/180*this.angle/2;
        var a = Math.sqrt( this.r*this.r / (5+4/Math.tan(beta)+1/(Math.tan(beta)*Math.tan(beta))) );
        var b = a/Math.tan(beta);
        this.shp.graphics.drawRect( -1*a, -1*(2*a+b),2*a,2*a );
        this.shp.graphics.endFill();
    }
}

最终来看一下运行效果。