A闪的 BLOG 技术与人文

游戏中的数学

第2章 游戏中的数学

本章主要讲解一些2D游戏中常见的数学知识，在后面的章节中‌‌会使用到这些数学知识，‌‌以及本章所介绍的一些‌‌类‌‌。如果‌‌你熟悉相关的内容‌‌可以直接跳过本章阅读后面的内容。‌‌在后面的章节中当使用到本章所需要的内容时，‌‌也可以跳回本章，阅读相关章节。

‌‌2D游戏和3D游戏的数学‌‌所使用的‌‌数学知识‌‌完全不是同一量级，‌‌本书只讨论如何开发2D游戏，‌‌并不会涉及3D领域的内容。所以你会在本章当中看到诸如坐标系，‌‌多坐标系，三角函数以及向量相关知识，‌‌后面一些章节会涉及到矩阵，‌‌在本书当中不对矩阵做过多的详细讲解，‌‌你可以通过其他书籍以及‌‌网络‌‌查阅学习矩阵相关知识。‌

2.1 笛卡尔坐标系统

勒内·笛卡尔（Rene Descartes）生于公元1596年3月31日，是法国著名的哲学家、物理学家、数学家和神学家。这一节所要讲解的是笛卡尔在数学领域所创立的解析几何。在笛卡尔时代，代数是一个比较新的学科，几何学的思维还是当时数学界的主流理论。笛卡尔通过他的研究成功地将当时完全分开的代数和几何学联系到了一起。在1637年，创立了坐标系后，成功的创立了解析几何学。这一成就也为微积分的创立奠定了基础。

解析几何是一个非常重要的的数学思想方法。其中，平面直角坐标系是建立解析几何的基础。直角坐标系在代数和几何两个不同物种之间形成了一种转换的桥梁。我们可以将几何图形‘转译’代数方程式，从而将几何问题以代数方法求解。没有解析几何，也就不存在游戏中所谓的图形学。对于一个几何问题，我们也无法转换为一个代数公式，同时让计算机帮我们完成计算。

游戏中和图像相关的操作，如运动等都建立在解析几何之中。我们要透过分析，将几何问题转化为代数问题，并通过编码来实现。而所有的几何元素都建立在笛卡尔坐标系中。

笛卡尔坐标系（Cartesian坐标系或直角坐标系），是一种正交坐标系。二维的直角坐标系是由两条相互垂直、0 点重合的数轴构成的。在平面内，任何一点的坐标是根据数轴上对应的点的坐标设定的。

2.1.1 笛卡尔坐标系实例

我们日常生活中，最为常见的地图，就可以视作典型的笛卡尔坐标系的实际应用。

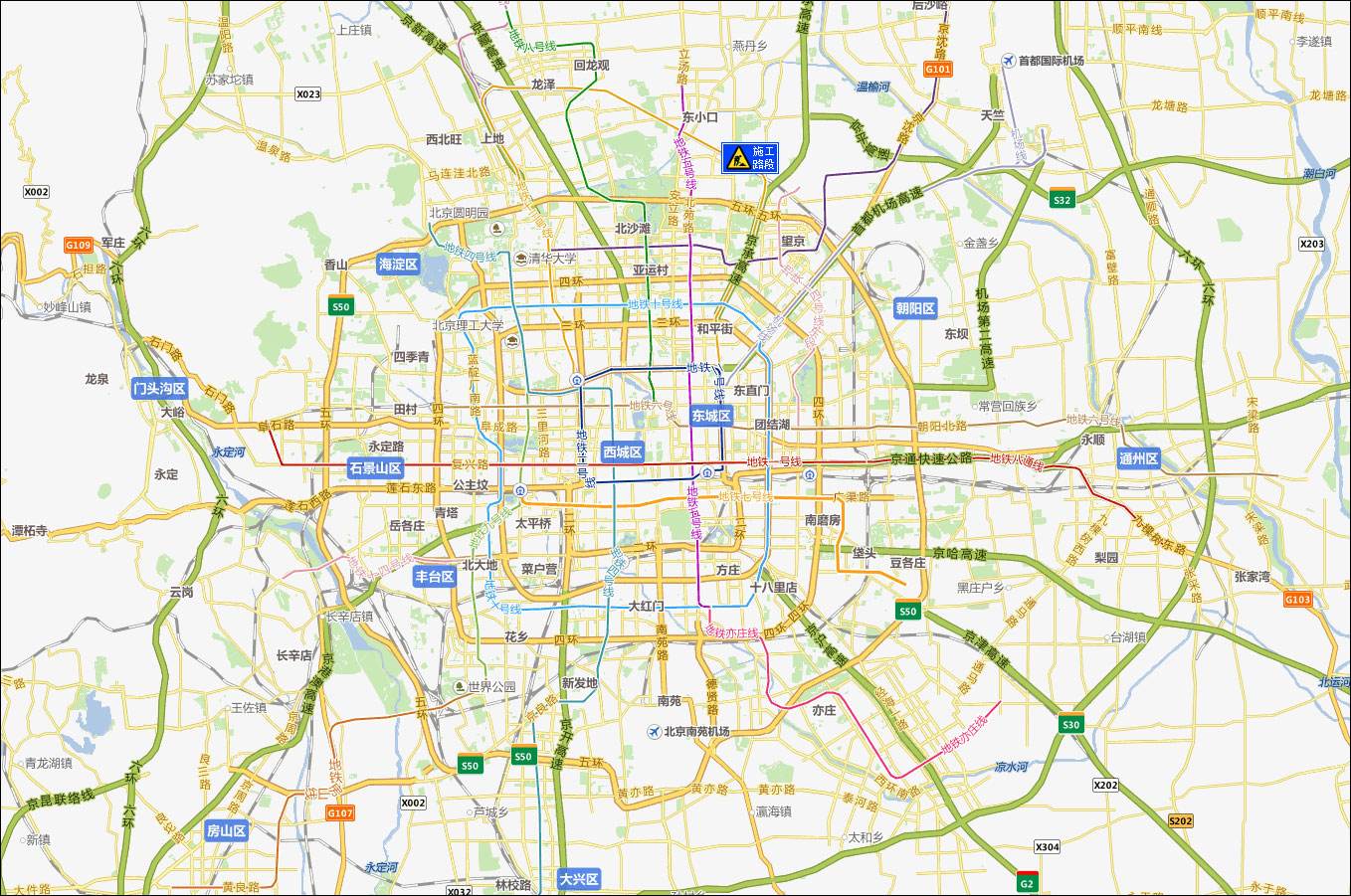
透过这张地图我们可以这样描述，北京天安门的中心是北纬39度54分，东经116度23分。其中的经纬度就是笛卡尔坐标系的两个互相垂直的轴。

2.1.2 2D坐标系的建立

我们在一张白纸上可以很快绘制出一个2D坐标系，如下图：

当前这个坐标系中，水平方向定义为x轴，同时方向向右x轴值变大。垂直方向定义为Y轴，方向向上y轴值变大。相交点为（0,0）点，也称之为原点（坐标原点）。

2D笛卡尔坐标系的定义有两点：

1. 每个2D笛卡尔坐标系都有一个特殊的点，叫做“原点”（Origin(0,0)）。它是坐标系的中心。
2. 每个2D笛卡尔坐标系都有两条过原点的直线并向两边无限延伸，叫做“轴”（axis）。两个轴互相垂直。

上图所示是笛卡尔坐标系的惯用法，2D中水平的称为“x轴”，垂直的称为“y”，同时方向如图所示。

小提示

在3D坐标系中，会多出一个“z轴”。用于表示物体的深度（也可以理解为物体的厚度）。

笛卡尔坐标系定义中并没有要求两个轴的方向是什么，也没有定位轴的计量单位是什么。所以在实际使用过程中，我们应该注意当前几何元素所处的坐标系是一个什么方向的坐标系。与此同时，你可以根据自己的需求定义坐标系。

下面列举几个坐标系在我们实际开发中的应用情况。

WebGL坐标系

HTML5中所使用的WebGL是OpenGL标准的子集，两者的坐标系是系统同的。其原点在屏幕中心，x轴是从左到右方向，y轴是从下到上方向。其z轴是垂直屏幕向外（z轴在3D中才会使用到，2D游戏中z轴会被锁定，本书不讨论与z轴相关知识点。）

它和笛卡尔坐标系惯用法的坐标方向一致，但其每个轴的单位不同。在创建WebGL环境后，我们需要为其输入一个屏幕尺寸，无论这个屏幕尺寸宽高是否相同其中心点到屏幕边缘的单位始终是1。示意图如下：

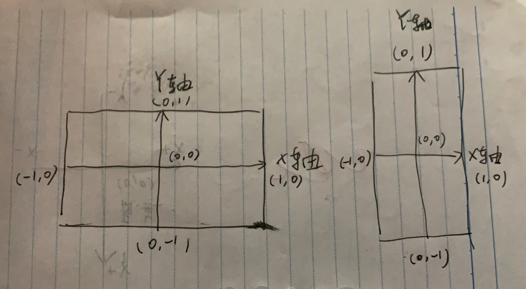
虽然方向相同但x轴和y轴的实际单位长度不同，这和我们平时的认知不太相同，但确实是WebGL标准中所规定的内容。

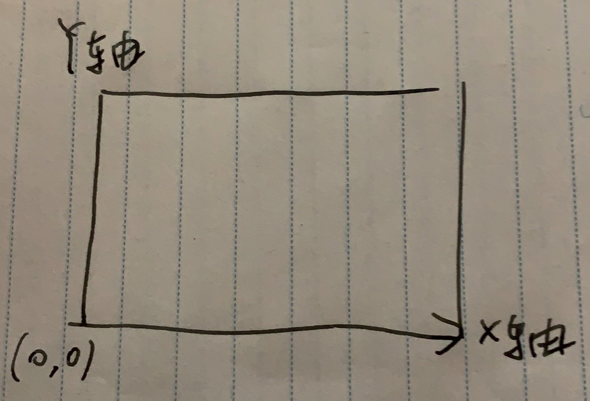
Cocos坐标系

Cocos引擎的坐标系也采用了笛卡尔坐标系的惯用法，但它定义原点位于屏幕的左下角。也就是说当一个点的x轴或者y轴小于0的时候，则表示该点已经超出屏幕区域。示意图如下：

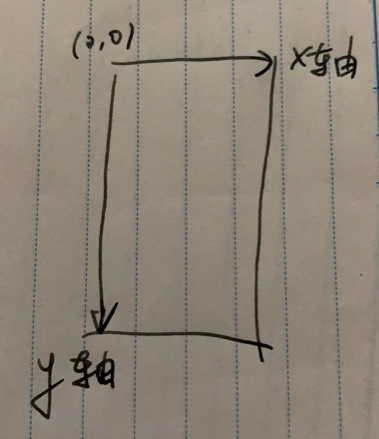
Egret坐标系

Egret引擎的坐标系和系统屏幕的坐标系以及网页的坐标系方向一致。它的坐标原点位于屏幕左上角，同时y轴的方向是从上到下变大。和笛卡尔惯用法的方向不一致。示意图如下：

几种坐标轴的表示方法并没有好坏之分，因为无论如何我们都可以借助数学工具对坐标轴进行转换，从而达到我们想要的坐标轴系统。不同的方向和单位在进行计算上肯定会稍有不同，例如：当我们制作一个雪花飞落的动画时。使用Cocos引擎需要对雪花的y轴进行减法操作，而Egret引擎则需要对y轴进行加法操作，区别仅此而已。

小提示

至此开始，我们所有描述2D空间位置信息的方式均采用Egret引擎中的坐标系方向。其目的是让大家熟悉并形成习惯。避免在后面的章节中，因为坐标系方向理解错误而导致的计算错误。

总体来说，无论x轴和y轴选择什么方向，总是能通过旋转使得x轴向右为正，y轴向上为正。从某种意义上讲，所有的2D坐标系都是“等价”的。

注意

如上等价这种说法在3D坐标系中不成立，3D坐标系中的左手坐标系和右手坐标系并非等价，也无法通过数学转换得到一致结果。

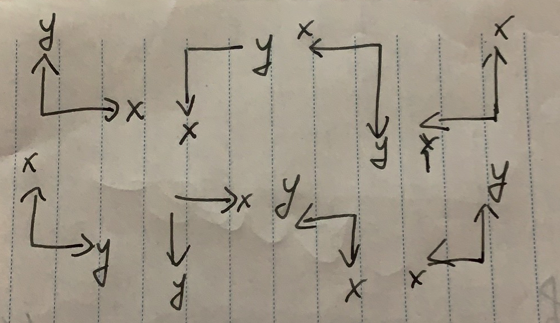
以下是坐标轴的8种方向，你可以自己尝试旋转每一个坐标轴，让他的方向与笛卡尔坐标系惯用法一致。

2.1.3 2D笛卡尔坐标系中的点

笛卡尔坐标系是一个精确定位点的框架，通过引入笛卡尔坐标系，我们可以精确的描述一个点所在2D平面中的位置。使用两个数（x，y）就可以定位一个点。例如，在2D笛卡尔坐标系中，点（3,2）所处的位置如图：

上图中点（3，2）中，x表示点到y轴的有符号的距离，y表示点到x轴有符号的距离。“有符号的距离”是指在魔偶个方向上距离为正，而在相反方向上距离为负。

2.1.4 Egret引擎中的Point类型

在已知数学概念后，对应Egret引擎中对点的封装是Point类，Point用来表示2D笛卡尔坐标系中的点。你可以在API文档中找到egret.Point的相关描述。如果用代码来表示上一节中的点（3，2）可以使用如下代码：

let point:egret.Point = new egret.Point(3,2);
console.log("x轴:", point.x, "\ny轴:", point.y);

运行代码，可以在浏览器控制台中看到打印内容：

x轴: 3
y轴: 2

除次以外Point类还为我们提供了一些其他常用的功能，如offset方法可用来做点的位置偏移，equals方法可用检查两个点位置是否相同等等。在本章后面的小节中我们还会遇到相关的数学问题以及如何借助Point类来进行计算。

2.2 多坐标系

2.2.1 为什么要使用多坐标系

通过前面一小节的学习，我们了解到笛卡尔坐标系的重要之处。游戏画面中每一个物体的位置信息，都通过坐标系来进行描述。在实际的游戏开发中，我们会使用多个坐标系。为什么要使用多坐标系呢？当我们创建一个游戏场景，即宣布这个场景的坐标系属于世界坐标系。所有的物体所有的点都在使用这个坐标系描述不同很统一么？不！

当我们使用一个坐标系来描绘整个场景的时候，场景中的任意点都可以用该坐标系描述，此时如果有一只狗一遍摇动着耳朵，一边走，这个时候如果进行坐标的转换会发现异常的麻烦。你在修改狗的位置的同时，还要计算其耳朵的位置并且将耳朵再进行旋转，让他有摇动的效果。此时如果我们把狗看做整体，狗的移动问题就可以用这个坐标系解决，但是这狗还摇动耳朵，这时候我们应该以狗为坐标系，狗的耳朵移动是在狗这个坐标系的基础上就简单多了。

上面这个例子总结起来很简单，当两个物体之间的运动是相对的时候，我们就应该将他们放到一个独立的坐标系中。这样只需要计算他们在这个坐标系里所做的运动或改变。而这个独立的坐标系再相对于世界坐标系做运动或改变。这样我们就将一个复杂的问题进行拆分简化，每次只需要关心他们坐标系“内部”的变化即可。

你可能觉得单单位置移动即使使用世界坐标系也不成问题。确实，如果是单纯的做位置平移那问题还真是简单，一旦加入物体的旋转，以及过多的相对关系。针对单一坐标系的计算将成为大麻烦。想象一下牵线木偶吧，如果要对这个木偶做奔跑的动作，每一个部件都针对世界坐标系来计算，可想而知有多麻烦。

每一个部位都要根据上一个部位的位移和旋转结果再做运算，从脚步到小腿再到大腿，一直延伸到身体。每一次都要经过位置和旋转的计算，从而得到他们连接点的位置和角度。

所以，安心的接受多坐标系吧。

2.2.2 世界坐标系

世界坐标系‌‌又叫全局坐标系，‌‌它是一个特殊的坐标系。它建立了‌‌一个描述其他坐标系所需要的参考框架。‌‌从另外一方面讲，‌‌用世界坐标系能够描述其他坐标系的位置。世界坐标系是我们建立的最大坐标系，Egret引擎在初始化时已经为我们创建了一个默认的世界坐标系，你无法修改它只能按照已设定好的规则运行。

2.2.3 物体坐标系

物体坐标系是和物体相关联的坐标系，‌‌我们每创建一个‌‌物体，它都有独立的坐标系，‌‌当这个物体移动‌‌或者‌‌旋转角度发生改变的时候，‌‌该物体和其关联的坐标系‌‌也随之发生改变。‌‌例如，‌‌我们在舞台上绘制一辆汽车，‌‌当这个汽车‌‌向前移动或者向后移动的时候，‌‌他的坐标系也跟随向前，或者向后移动。

在Egret引擎中，最为常见的‌‌物体坐标系‌‌是矢量绘。‌‌当我们创建一个矢量图元素时，‌在里面画一个‌‌圆形，‌‌此时需要输入圆心位置和‌‌圆形半径的长度，‌‌圆心位置就在当前这个矢量图对象的物体坐标系当中。设置完成后可以绘制出一个圆形。当我们移动这个物体‌‌的时候，‌‌这个圆形也会跟随移动，其物体坐标系也会随着‌‌发生变化。

2.2.4 惯性坐标系

惯性坐标系是人为创造出来的一种坐标系，它的位置和物体物体坐标系重叠。创造这样一个坐标系的目的是方便我们从全局坐标系到物体坐标系进行转换。

当需要将一个点从全局坐标系转到物体坐标系时，首先先转换到惯性坐标系中。因为此操作只需要进行位移即可。然后再从惯性坐标系到物体坐标系，这个操作只需要旋转即可。将世界坐标系与物体坐标系的转换，从位移加旋转‌‌拆分成两部分，‌‌这样的好处在于计算‌‌变得非常的简单。

2.2.5 嵌套式坐标系

在使用Egret引擎时，你无时无刻不在使用嵌套式坐标系。当你想画面中添加了一个图片后，这个图片即可和跟容器形成了嵌套关系。图片自身带有一个物体坐标系，而你的跟容易也带有一个物体坐标系。两者之间形成嵌套关系。你还可以使用Egret引擎中的DisplayObjectContainer类（第6章显示编程会讲到）直接创建一个容器，这个容器自带一个物体坐标系，可以向里面放入其他的图片等容。这也形成了嵌套关系。

嵌套式坐标系的好处在于，我们通过嵌套关系，将多个物体坐标系组合到一起。通过改变它们父级的坐标系来进行整体移动旋转和变换。在后面的章节中，你会体会到嵌套式坐标系所带来的种种好处。

2.2.6 坐标系转换

坐标系转换需要一套复杂的公式，单独通过示意图可以清楚的解释其中的计算方法。但在Egret引擎内部，所有坐标系使用Matrix（矩阵）来表示，而矩阵的运算又难以理解。这里仅介绍两个内置的转换坐标系的API。

Egret引擎中，能够看到的物体均继承自DisplayObject（现实对象）类。这个类中包含了一个Matrix属性，用来保存当前物体的物体坐标系。当需要将一个点从全局坐标系转换到这个物体坐标系时，可以使用globalToLocal方法。其方法定义如下：

public globalToLocal( stageX:number,stageY:number ,resultPoint:egret.Point ):egret.Point

前两个参数为全局坐标系中一个点的x轴和y轴的值，resultPoint是转换后的结果。第三个参数是为了节约内存使用，将计算后的结果直接赋值给实参。

另外一个API是反向转换，将一个点从物体坐标系转换到全局坐标系。方法为localToGlobal，方法定义如下：

public localToGlobal( localX:number,localY:number ,resultPoint:egret.Point ):egret.Point

前两个参数为物体坐标系中一个点的x轴和y轴的值，resultPoint是转换后的结果。

2.3 三角函数

人类对三角函数的研究远比坐标系要早的多。中国古代就有勾股定理（勾三股四弦五），如果读者有兴趣可以查阅古希腊数学家欧几里得所著的一部数学著作《几何原本》，内容包括大量几何定义和公理。本接不讲解那些公理，仅讨论所需要的三角函数相关内容。

2.3.1 三角函数定义

三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。也可以等价地用与单位圆有关的各种线段的长度来定义。三角函数在研究三角形和圆等几何形状的性质时有重要作用，也是研究周期性现象的基础数学工具。常见的三角函数包括正弦函数、余弦函数和正切函数。在程序开发中，还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。不同的三角函数之间的关系可以通过几何直观或者计算得出，称为三角恒等式。

正弦

正弦（sine），在直角三角形中，任意一锐角∠A的对边与斜边的比叫做∠A的正弦，记作sinA，即sinA=∠A的对边/斜边。

在上面的图中，sinA=a/c。JavaScrpit中，对于正弦计算可使用Math.sin(x)函数。参数x为一个以弧度表示的角,返回值是x的正弦值，取值范围在-1.0到1.0之间。

余弦

余弦（cosine），在直角三角形中，任意一锐角∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA=∠A的邻边/斜边。

在上面的图中，cosA=b/c。JavaScrpit中，对于正弦计算可使用Math.cos(x)函数。参数x为一个以弧度表示的角,返回值是x的余弦值，取值范围在-1.0到1.0之间。

正切

正切（tangent），在直角三角形中，任意一锐角∠A的对边与邻边的比叫做∠A的正切，记作tanA，即cosA=∠A的对边/邻边。

在上面的图中，tanA=a/b。JavaScrpit中，对于正弦计算可使用Math.tan(x)函数。参数x为一个以弧度表示的角,返回值是x的正切值。

程序中的三角函数

上面所讲的三角函数是在数学中的定义，与此同时JavaScript中除了对正弦余弦正切运算的支持，还提供另外三种反向运算。

反正弦函数Math.asin(x)，参数x是一个取值范围在-1.0到1.0之间的数。其返回值是x的反正弦值。表示-PI/2到PI/2之间的弧度值。

反余弦函数Math.acos(x)，参数x是一个取值范围在-1.0到1.0之间的数。其返回值是x的反余弦值。表示0到PI之间的弧度值。

反正切函数Math.atan(x)，其返回值是x的反正切值。表示-PI/2到PI/2之间的弧度值。

通过以上3个反向运算函数，我们可以通过运算准确得到对应的弧度。

2.4 向量

我见过很多游戏开发新手甚至是老手都会忽略向量这个强有力的工具。在处理2D游戏的一些运算时，确实可以使用其他方式来取代向量，但统一数学工具会对开发有着莫大好处。

2.4.1 向量的基本定义

计算机绘图、碰撞检测和物理模拟是现代视频游戏的基本组成部分，向量（vector）在这些领域中具有至关重要的作用。向量是一种同时具有大小和方向的物理量。同时具有大小和方向的物理量称为向量值物理量。常见的向量值物理量有：力（在某个特定方向上施加一定的作用力——量值），位移（在某个净方向上移动一段距离），速度（速率和方向）。因此，向量可以用来表示力、位移和速度。有时我们也用向量来表示一个单个方向。

首先，我们从几何学角度描述向量的算术特征：我们通过一个有向线段来表示向量（如下图），其中长度表示向量的大小，箭头表示向量的方向。我们注意到，向量所描绘的位置并不重要，改变向量的位置并不会影响向量的大小和方向（这是向量具有的两个属性）。也就是，当且仅当两个向量具有相同的长度和方向时，我们说这两个向量相等。

遗憾的是Egret中并没有提供向量类，我们需要自己去封装一个名为Vector的类，来进行向量相关的操作。

注意

Egret引擎中存在一个名为Point的类，这个类看上去和向量非常相似，但它仅用来表示二维空间坐标系中的点，而非向量。

2.4.2 向量的表达与类定义

提示

当前我们只讨论二维空间中的向量，向量中只存在x轴和y轴两个维度。

向量中的数表示了每一个维度上有方向的位移。例如，沿x轴移动3像素，沿y轴移动5像素。那么这个向量可以表达为[3,5]。如果用程序来表示的话，可以使用数组。但最好还是通过属性封装的方式来定义。

下面的代码建立了一个Vector类，用来表示向量，其包含名为x,y的两个属性，用来表示该向量在两个坐标轴上的大小。

class Vector {
    public x: number;
    public y: number;

    public constructor(x: number = 0, y: number = 0) {
        this.x = x;
        this.y = y;
    }
}

如果创建了一个Vector对象，并将其x属性设置为10，y属性设置为20，那么表示的含义是什么呢？

let v:Vector = new Vector( 10, 20 );

将这个动作进行拆解，可以理解为，沿x轴移动10像素，沿y轴移动20像素。这样去理解向量相比于其他方式就简单许多，如图。

2.4.3 零向量

零向量是一个非常特殊的向量，它的每一个轴的位移都为0。你可以将其理解为没有方向，没有距离。在Vector类初始化的时候它确实为一个零向量（如果你不为其构造函数出入任何值）。零向量理解并不困难，之所以在这里描述零向量是因为在后面的向量运算中，会出现向量元素作为除法除母的问题。遇到该情况，当前四则运算不成立会导致程序出错。

2.4.4 向量的模（长度或大小）

向量是描述有大小和方向物理量，但到目前为止，我们所定义的x和y即不是向量的大小，也无法用它们来描述向量的方向。这里需要通过计算来获取一个向量的大小（模和长度与大小概念相同）。

借助 2.4.2 节中的示意图，可以得出向量的大小实际上就是图中所构成的直角三角形的斜边长。在透过结合勾股定理即可推算出公式，即：

向量的模^2 = x^2 + y^2

向量的模 = 开方（x^2 + y^2）

在Vector类中，可以定义norm方法，用以计算向量的模。

public get norm(): number {
	return Math.sqrt(this.x * this.x + this.y * this.y);
}

2.4.5 向量的平移（向量加法）

向量与向量之间是可以做四则运算的，但前提在于它们的维度相同。当一个物体运动时，它的运动方向与大小使用向量[2,3]来表示。此时又出现另外一个力，这个力用向量[5,1]来表示。两个力合作用在这个物体上，那么它的运动方向和大小应该是多少呢？

这种情况属于向量的平移，只需要将两个向量做加法运算即可。如果用几何来描述向量的平移，两个向量首尾相接的结果，该结果也是一个向量。向量加法的公式如下：

A + B = ( X1+X2, Y1+Y2 )

换成几何图形解释如下图：

向量a + 向量b = 向量c

在程序中只需要将向量的两个轴的值分别相加即可，从而得到一个全新的向量。继续来扩展Vector类，使其支持向量加法运算。

public static add(v1: Vector, v2: Vector): Vector {
	return new Vector(v1.x + v2.x, v1.y + v2.y);
}

2.4.5 一个点到另一个点的向量（向量减法）

计算一个点到另外一个点的位移类似于沿着一个路径移动，可以用向量减法运算来得到新向量。在几何中可以描述为，两个向量结尾相连的结果，该结果也是一个向量。

向量减法的公式如下：

A - B = ( X1-X2, Y1-Y2 )

换成几何图形解释如下图：

向量a - 向量b = 向量c

在程序中只需要将向量的两个轴的值分别相减即可，从而得到一个全新的向量。继续来扩展Vector类，使其支持向量减法运算。

public static subtract(v1: Vector, v2: Vector): Vector {
	return new Vector(v1.x - v2.x, v1.y - v2.y);
}

2.4.5 改变向量大小（向量与标量相乘）

数学概念上，标量是表示平时所用的数，例如5，是一个标量。标量无法与向量做加减操作，但却可做乘法运算。其运算法则为标量分别乘以向量每一个维度的值。

在做完乘法之后，从几何意义上来解释实际上是改变了向量的大小，而标量成为大小改变时的系数。假如我们想将一个向量的大小扩大2倍，那么直接乘以标量即可。公式如下：

Ab = ( X1b, Y1b )

添加对标量乘法的支持，代码如下：

public multiply(s: number): void {
	this.x *= s;
	this.y *= s;
}

提示

你可以将一个向量乘以一个标量，然后打印出运算前后的长度值。查看向量的长度是否是运算前的倍数关系。

2.4.6 负向量

所谓负向量是指和当前向量大小相同，但方向相反的向量。将一个向量变成负向量，需要对其每一个轴的大小进行方向翻转操作即可。

为了得到一个向量的负向量，我们可以直接将当前向量乘以标量-1即可得到正确结果。在Vector类中添加对负向量的操作支持。

public negative(): void {
    this.multiply(-1);
}

2.4.7 向量的归一化（标准化）

很多时候我们要在游戏中使用向量来表示一个物体的方向，而不关心其大小。这样情况下使用“单位向量”将非常方便。所谓单位向量就是大小为1的向量。将一个向量变成单位向量的操作我们称之为归一化，也叫做标准化。

归一化的操作要求是不改变向量的方向，只将其长度改为1。借助向量与标量的乘法操作即可实现。例如一个向量的长度为5，那么我们就将它乘以1/5即可得到单位向量。

注意

当一个向量的长度为0时，该向量为零向量。做运算时其分母为0，导致除法运算错误。

实现代码如下：

public normalize(): void {
	if (this.norm === 0) {
		return;
	}
	this.multiply(1 / this.norm);
}

2.4.8 向量的点乘

向量可以和标量相乘，向量也可以与向量相乘。但向量相乘有两种不同乘法，本小结介绍其中一种，叫做点乘（内积或数量积）。点乘的公式表示为：A·B。与标量与想向量乘法一样，点乘的优先级高于加减法。点乘的运算公式是对应维度分量乘机的和，其结果是一个值。分解后结算公式与做用如下。

A·B = X1X2 + Y1Y2

点乘所得到的结果蕴含的信息非常重要，它反映着两个向量的“相似度”，两个向量越“相似”，它们的点乘越大。

如果 A·B = 0，那么表示两个向量互相垂直，其夹角为90度。如果 A·B < 0，则表示两个向量夹角大于90度。相反，如果 A·B > 0，那么表示两个向量夹角小于90度。为了方便记忆，我们将上面三种情况总结为三个公式。

A·B = 0, 𝛳 = 90°

A·B < 0, 𝛳 > 90°

A·B > 0, 𝛳 < 90°

𝛳 为两个向量的夹角。

在程序中实现点乘函数，代码如下：

public static dotProduct(v1: Vector, v2: Vector): number {
	return v1.x * v2.x + v1.y * v2.y;
}

2.4.9 计算两个向量的夹角度数

借助点乘我们可以计算两个向量之间的夹角度数，前面我们能够透过点乘结果来判断三种结果，但要计算精确的夹角度数，还需进一步计算。在这个计算中，我们需要使用向量的模。向量点乘的结果也等于向量大小与向量夹角cos值的积，公式书写如下：

A·B = A的模 × B的模 × cos𝛳

将公式进行推导，求𝛳角度的值，推导结果如下：

代码实现如下：

public static angle(v1: Vector, v2: Vector): number {
	let a: number = Vector.dotProduct(v1, v2);
	let b: number = v1.norm * v2.norm;
	let c: number = a / b;
	let rad: number = Math.acos(c);
	let deg: number = rad * 180 / Math.PI
	return deg;
}

注意

当前函数计算后返回值为角度值。

2.4.10 向量投影

借助点乘我们还可以计算一个向量在另一个向量上的投影。通过上面一小节，我们能够借助点乘计算出两个向量的夹角度数。而计算投影，则需要借助这个夹角来进行计算。

假设a和b两个向量做点乘运算，

向量a·向量b=| a |*| b |*cosΘ

Θ为两向量夹角

| b |*cosΘ叫做向量b在向量a上的投影 | a |*cosΘ叫做向量a在向量b上的投影

代码实现如下：

public static projection(v1: Vector, v2: Vector): number {
	let a: number = Vector.dotProduct(v1, v2);
	return a / v2.norm;
}

2.4.11 向量的叉乘

向量的叉乘（也称之为向量积）公式表示为A×B。点乘的结果得到的是一个值，而叉乘的运算结果将得到的是一个全新的向量。这个全新的向量将垂直于两个原始向量。叉乘仅适用于3D领域，故在本书中不做过多讲解。

2.4.12 向量类中一些方便的接口

在Vector类中，我们加入一些方便程序开发的接口，这些接口和向量定义与运算没有直接关心，仅仅是为了方便我们使用而定义的。由于接口都比较简单，不再做过多赘述。你只需要查阅每个函数的注释即可立即明白它的作用。

/**
 * 复制另外一个向量的值
 */
public copy(v: Vector): void {
    this.x = v.x;
    this.y = v.y;
}

/**
 * 设置向量的值
 */
public setTo(x: number, y: number): void {
    this.x = x;
    this.y = y;
}

/**
 * 新建一个向量，Vector(1, 1)
 */
public static one(): Vector {
    return new Vector(1, 1);
}

/**
 * 新建一个向量，Vector(0, 0)
 */
public static zero(): Vector {
    return new Vector(0, 0);
}

/**
 * 新建一个向量，Vector(-1, 0)
 */
public static left(): Vector {
    return new Vector(-1, 0);
}

/**
 * 新建一个向量，Vector(1, 0)
 */
public static right(): Vector {
    return new Vector(1, 0);
}

/**
 * 新建一个向量，Vector(0, 1)
 */
public static down(): Vector {
    return new Vector(0, 1);
}

/**
 * 新建一个向量，Vector(0, -1)
 */
public static up(): Vector {
    return new Vector(0, -1);
}